広島カープの投手応援歌に「振らな何も始まらないから」というフレーズがあります。
バッティングは本業ではないピッチャーでも、バットを振れば何か起きるかもしれない。
とても素敵な歌詞だと思います。(私は横浜ファンですが・・・)
ところで「振らなきゃ当たらない」って、似たような言葉をどこかで聞いたことがあります。

そう、宝くじ(を買う人の言い訳)です。
買っても当たらないものを何故買うのか。
それは、くじの1枚1枚には億万長者の夢が詰まっているからなのでしょう。
つまり、夢を買っているのですね。
とはいえ、お金を賭けることはギャンブル行為です。
競馬や競艇よりは聞こえが良いかもしれませんが、宝くじだってギャンブルと言わざるを得ません。
さらに、宝くじは「割に合わない」とよく言われます。
ギャンブルの「割の良さ」は還元率で話されることが多いですが、宝くじはその他の賭け事よりも還元率が低いとのこと。
バットを振らなければ何も始まらないのは、たしかにそうですが、やみくもに振れば良いというわけではないはず。
今回は「宝くじは本当に割に合わないギャンブルなのか」をテーマに記事を書きます。
たしかに宝くじの還元率は低い
還元率ってなんだ?
まず大前提として、どのギャンブルにも必ず胴元がいます。
競馬のJRA(日本中央競馬会)などが有名ですね。
宝くじの発売元は地方自治体で、銀行が販売・広報などを委託されているとのことです。(はじめて知りました・・・)
各ギャンブルごとに胴元の取り分(控除額)の割合はおおよそ決まっています。
売上金額から控除額を引いて、残った金額が賭けた人に還元される仕組みというわけです。
よって、還元率は次の式で表されます。
ギャンブルの還元率
還元率 = (売上金額 ー 控除額) ÷ 売上金額
還元率75%のギャンブルに100円を賭けることを繰り返すと、平均の払戻金額は75円になります。
つまり、「還元率×100=期待値」と言えますね。
いろいろなギャンブルと比較してみる
それでは、宝くじの還元率をいろいろなギャンブルと比較してみましょう。
総務省のHPで還元率(参考値)についての記載がありましたので、次の図にまとめてみます。
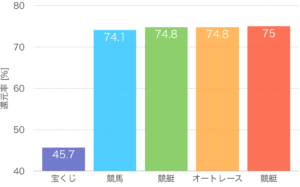
宝くじの還元率は45.7%という驚異的な低さ。
1枚300円を買い続けても、理屈では平均で137円しか返ってこない、悲惨な結果に終わります。
他のギャンブルの還元率と比較してみても、宝くじは割に合わないギャンブルと言えそうです。
「夢を買っている」の意味を考える
長蛇はジャンボな夢を見る
還元率だけを見ると、宝くじはあまりにも割に合わないギャンブルです。
それでも夏や年末には宝くじ売り場に長蛇の列ができます。
割に合わないギャンブルを何故やるのか。
それは、長蛇を作る彼/彼女らが「夢を見ている」からなのです。

では、長蛇の見る夢は何者なのでしょうか。
夢の正体は「ボラティリティ」
宝くじが他のギャンブルと異なる点のひとつは、「ボラティリティ(標準偏差)が圧倒的に大きいこと」です。
ボラティリティー(Volatility)とは、一般的に価格変動の度合いを示す言葉で、「ボラティリティーが大きい」という場合は、その商品の価格変動が大きいことを意味し、「ボラティリティーが小さい」という場合は、その商品の価格変動が小さいことを意味します。現代ポートフォリオ理論などでは、このボラティリティーを標準偏差で数値化し、それをその商品のリスクの度合いとして捉えるのが一般的です。つまり、ボラティリティーが大きい商品はリスクが高く、ボラティリティーが小さい商品はリスクが低いと判断されるのが通常です。
標準偏差で算出したボラティリティーが大きい場合、実際のリターンと期待収益率(予想されるリターンの加重平均値)とのブレが大きくなる可能性が高いことを意味しています。そのような価格変動のブレの大きい商品は、多くの人が避けることから、一般にリスクが高いと判断されます。
ボラティリティが大きいということは、実際の当せん金額と期待値(平均値)の差が大きいということ。
逆に言えば、ボラティリティが小さい時には期待値通りの収益になりやすいということですね。
例として、2019年の年末ジャンボの当選金額(1ユニット換算)は、次の表の通りになります。
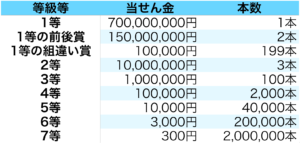
(2019年年末ジャンボを1ユニット換算したもの ※1ユニット2,000万枚)
こちらの表から、宝くじを1枚買った時の「確率・期待値・分散・標準偏差」を計算したものが次の表になります。
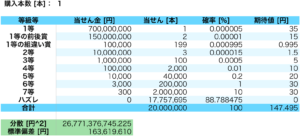
ボラティリティ(標準偏差)は「163,620円」です。
ただ、これだけだと大きいのか小さいのか、よく分かりませんね。
ちょうど同じ時期に開催された、2019年の有馬記念を比較対象として見てみましょう。
簡単のため、単勝(1着の馬を的中させる)の場合を考えてみます。
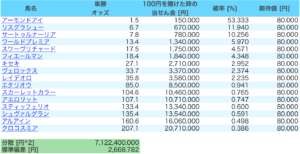
(当せん確率は「単勝還元率0.8/単勝オッズ×100」で計算)
単勝に100円を賭けた場合、ボラティリティは「2,669円」となりました。

宝くじのボラティリティの大きさが、長蛇に見せる「夢」の正体なのではないでしょうか。
夢には効率的な買い方がある
買えば買うほど当たりやすくはなるけど・・・
私の母は年末になると、よく宝くじを大量に買ってきます。
「買わなきゃ当たらない」けれど、大量に買えば良いってものではないでしょう・・・と幼い頃からよく思っていました。
当然のことですが、宝くじを全て買い尽くすことができれば、100%当せんしますね。
しかし、宝くじの還元率は45.7%なので、100%当せんするということは54.3%の損失を確実に出すことを意味します。
では、何枚買うのが、効率よく夢をみることができるのでしょうか。
購入枚数とボラティリティの関係を視覚化してみる
2019年の年末ジャンボで1等・前後賞を狙って連番で購入することを考えます。
(こちらのサイト様のシミュレーションを参考にさせていただきました!良記事ありがとうございます。)
先述の通りですが、2019年・年末ジャンボを1枚買った時のボラティリティは163,619円でした。

購入枚数を増やした時の、この数字の変化を見てみましょう。
連番で2枚買う
連番で2枚のくじを買う場合、1等に当せんすると前後賞のどちらかも確実に当せんすることになります。
そのため、「1等+前or後」に当せん金をまとめて、「前or後」の当せん本数を1つ減らして考えます。
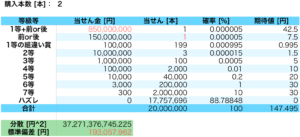
(※組違いより下については、簡単のために1枚の場合と同じにしています。興味のある方は「非復元抽出の確率」で調べてみてください!)
この場合のボラティリティは193,058円と、1枚だけ買うパターンよりも大きくなりました。
当たった時の金額が大きくなるので、当然ですね。
連番で3枚買う
連番で3枚のくじを買う場合、1等+前後賞が当たるのが1通り、1等+前or後賞が当たるのが2通り、1等の前後賞のみが当たるのが2通りになります。
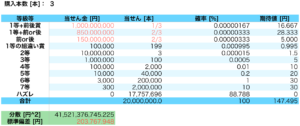
この場合のボラティリティは203,768円と、2枚だけ購入するパターンよりも大きくなりましたが、ボラティリティの増分は1枚→2枚よりも小さくなっています。
連番でn枚(≦10)買う
連番でn枚のくじを買う場合、購入枚数とボラティリティの関係は次のグラフのようになります。
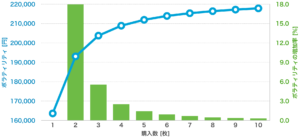
注目したいのは、購入枚数が増えるとボラティリティの増加率が下がっていく点です。
購入枚数が5枚を超えたあたりから、ボラティリティ(夢の大きさ)は頭打ちになっていくことが分かります。
連番で3〜5枚くらいを買うのが効率的な買い方と言えるのではないでしょうか。

まとめ
「宝くじは本当に割に合わないギャンブルなのか」
- 宝くじと他のギャンブルを還元率で比較すると、たしかに割の合わないギャンブルである。
- 宝くじの「夢」の正体は高いボラティリティである。
- 宝くじの購入枚数が増えるとボラティリティの大きさは頭打ちになる。連番で3〜5枚を買うのが効率的である。